AOJ0310 枠
この高速化テクは典型らしいです。
問題
のグリッドがあり、各マスに数が書かれている。
このグリッドに太さ1マス分の長方形の枠をのせ、枠が覆っているマスの数の総和を最大化する。
ただし、枠は や
や
のように、中央に穴が空いていない場合もある。(詳しくは問題文の図を見て)
制約
想定TLE
累積和をしてから、枠の左上と右下を全探索( )して、それぞれの枠についての総和をO(1)で求め、最大値を答える。
2次元累積和+長方形領域の総和を求めるパートくらいバグらせずに素早く書けるようにしましょう。
ちなみにこの問題を見た当初は 300^4くらいいける!w と思って書いてTLEしました(バカかな?)
解法
累積和して区間の総和を で求めるのは変わりません。
しかし、枠の4辺を全探索すると で間に合いません。
に落としたいので、とりあえず2辺を
で全探索して、残り2辺を
で決めることにします。
ここで、2辺を でしようとしたときに、しゃくとりを思い浮かべると、対辺をペアにするという発想ができます。
上下と左右、どっちを全探索しても本質的には同じなので、ここでは上下を全探索することにします。
行目を上の辺、
行目を下の辺として、総和が最大になるように右辺(
)と左辺(
)を決めます。
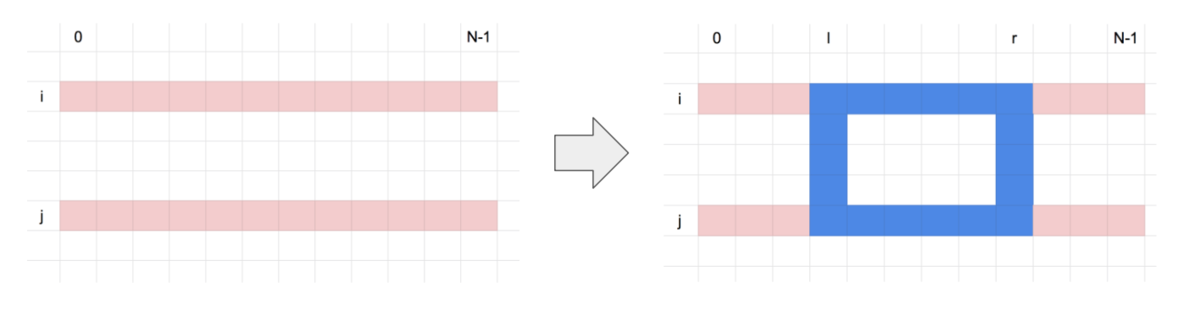
まず 行目と
行目を採用することは決まっているので、
行目と
行目のマスの総和を計算しておきます。ここでは、枠を決めたときのその総和からの差分を最大化していきます。
右辺と左辺を一度に考えるのは難しいので、先に右辺から考えます。
右辺を 列目にすると決めたとき、
行目の
列目以降の部分
行目の
列目以降の部分
は、枠には関係ない部分なので、不要になります。
逆に、
列目の
行目から
行目の部分
は枠の一部なので必要になります。

よって
( 列目の
行目から
行目の部分) - (
行目の
列目以降の部分) - (
行目の
列目以降の部分)
を計算してあげればよいです。
これを のすべての
について求めてあげます。
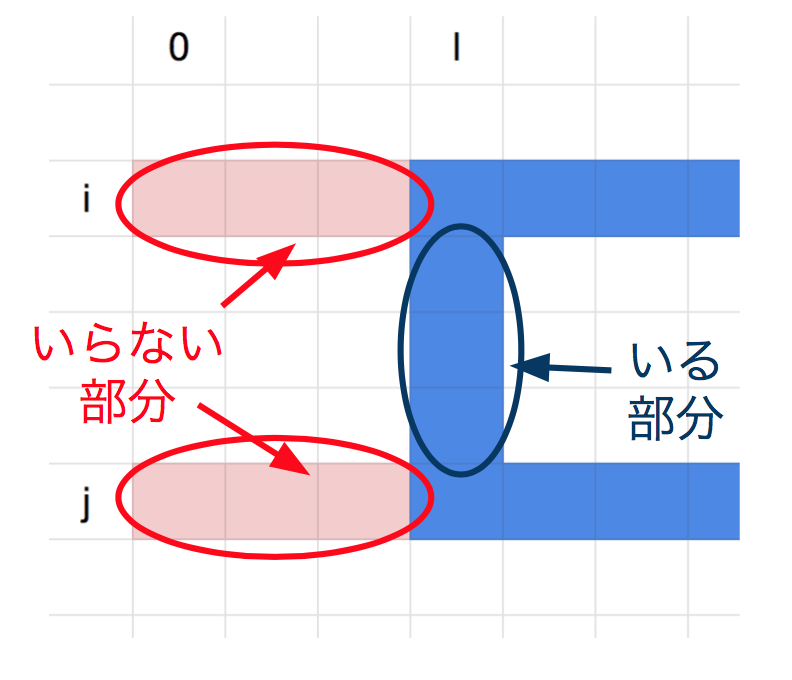
そして、左辺の についても同様で、
行目の
列目より前の部分
行目の
列目より前の部分
は、枠には関係ない部分なので、不要になります。
逆に、
列目の
行目から
行目の部分
は枠の一部なので必要になります。
よって
( 列目の
行目から
行目の部分) - (
行目の
列目より前の部分) - (
行目の
列目より前の部分)
を計算してあげればよいです。
これを のすべての
について求めてあげます。
これで前計算が終わったので、あとはこれらをうまく組み合わせて右辺と左辺を最適に選びます。
たとえば、 を決めると、最大となる
は、
をみたすもののうち、さっき計算した差分が最大となる
です。これは「右端が
列目以降であるときの最大値」などを前計算してあげると
で求められるので、右辺と左辺を計算するのは全体で
でできます。(実際は
の場合などは別で計算した方が簡単になります)