Googleスプレッドシートの書式設定で補助単位「X万XXXX」を出す
調べてもなかなか出てこなかったので苦労しました。
結論としてカスタム数値形式で
[>=10000]#"万"####;[<=-10000]#"万"####;0
を登録して必要なセルに適用させれば良いです。この式は「10000以上の場合は#"万"####の書式を使い、-10000以下の場合は#"万"####の書式を使い、それ以外は0の書式を使う」という意味です。
適用させると以下のようになります。

ちなみにセルの書式設定では条件を3つまでしか設定できないため、補助単位を多く使う場合などはTEXT関数を使うと良さそうです。
初心者による初心者のための家探しtips
そすうさ
・大学まで滋賀の実家暮らし、一人暮らし経験なし
・就職を機に上京
やったこと
・住みたい家の条件を考える
・家賃はこのくらいで、エリアはどこで、駅徒歩何分で、風呂トイレ別で、など
・スーモアプリなどで適当に検索していれば、どのくらいの家賃ならどのくらい妥協が必要かなどもわかる。家の条件には順位をつけて、「絶対外せない条件」と「できればほしい条件」などを明確にしておく
・そすうさの場合は、風呂トイレ別&2階以上&洗濯機が置けるは必須、オートロックや駅からの距離は優先順位が低かった
・不動産を予約する
・春はめっちゃ混む。1日で内見も契約もしたいなら朝から行くべき。
・最近はオンラインで内見ができたりもあるらしいから無理に行かなくてもいいとは思うけど、実際に内見にいくと家の周囲の状況(静かとか日当たりがいいとか)もわかる
・不動産にいく
・開凸して内見する家を探して、不動産屋の車で5軒回った。あんまり妥協せずに理想の物件をずっと探していたため、契約まで終わったのは夜7時くらいだった。(夕方遅くに内見に行くと家の周囲をあまり見れなくて残念な気持ちになる)
・内見にはメジャーを持っていって、ドアの幅や洗濯機置き場のサイズ、冷蔵庫のサイズなどをメモする。入居前に家具家電の目星をつけられるので。
・契約が終わると初期費用の話とか入居日の話とかをする。初期費用はだいたい家賃の2.5カ月分とか。入居前に審査があるので契約から入居までだいたい2週間以上かかる。初期費用は審査後に銀行口座に振り込む形。入居日は大家さんとも相談が必要なので、不動産で希望日を伝えて、あとから○月○日で確定です〜という連絡がくる。
・入居
・管理会社に行って書類を書いて鍵をもらう。印鑑を忘れたら詰むので注意。大家さんの立ち会いはなかったので、一人で家に向かう(実際は付き添いに来た家族もいた)。
・ガス、水道、電気など連絡する。ガスは立ち会いが必要なので注意。ガスは早くて当日夜から使えるようになる(連絡が遅いと翌日とか)。入居日がわかっていれば「○月○日に入居する」旨を事前に伝える方法もある。
・その日から住むのでベッドや布団、電球などを買って最低限夜を過ごせるようにする。
その他
・いいなーと思う物件があれば保存しておく。既に売れていたとしても、不動産の人に「こういう感じの物件がいいんですけど」と言えば雰囲気わかってくれる(実際にやった)
・もし余裕があれば、住みたいエリアが決まったら事前に行って雰囲気を確かめておくのがいいと思う。実は坂が多くて歩くのがつらいとか、駅前の商店街に店がたくさんあっていいとか、家探しの参考になったり上京後の生活が楽しみになったりする。(今年はコロナなので厳しそう)
・災害マップとか見ておくといいかも。賃貸だからそこまで気にする必要はないけど、川のそばとか、過去に浸水被害があったところで1階に住むのは怖い。
herokuのDB(無料)を使って競技プログラミングのアプリケーション開発
自分の用意したDBにコンテスト情報を入れて、情報の閲覧&追加ができるアプリケーションを作った。
→https://hackerrank-jp.herokuapp.com
DB周り
- まずherokuにappを登録する(名前を入力するだけでOK)
- コマンドラインで
$ brew tap heroku/brew && brew install herokuを実行してCLIを使えるようにする - その後は基本はこれ:無料でHerokuで簡単にDB[PostgreSQL]を作成する - ゼロからはじめるWEBプログラミング入門
ただ情報が古いのか違うところが多少ある。
DBの接続情報取得のところは heroku postgres

からsettingタブを開くとview credencialsがある
- view credencialsのページのHeroku CLIをコピーしてコマンドラインで実行するとDBに接続できる。多分初回は
The local psql command could not be located的なことを言われるので、そこで言われたリンク先のlocal setupをする。 - DBに接続できたら、
\lコマンドを打つとherokuに登録してあるdatabase全てが表示される。自分のdatabaseに入るには\c [database名](自分のdatabase名はview credencialsのページに載っている)を打てばよい。 - 自分のdatabase内で
\dt;(テーブルの一覧表示コマンド)を打つとDid not find any relations.と言われるはず。ここから好きにテーブルを定義して使う。
CREATE TABLE contest( contest_id serial, contest_name varchar(80), contest_url varchar(80), contest_date date, writer varchar(80) );
serialは連番型です。
urlはwww.hackerrank.com以下のコンテスト名だけ登録するようにします。
これを実行してから\d CONTEST;(CONTESTテーブルの情報を表示)するとテーブル構造が見れます。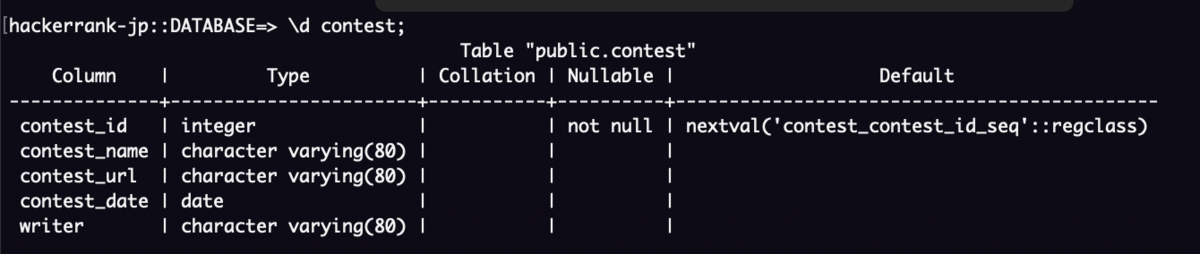
例えばこのテーブルに試しにhttps://www.hackerrank.com/yfkpo2を追加してみると、
INSERT INTO contest (contest_name, contest_url, contest_date, writer)
VALUES ('ゆるふわ競技プログラミングオンサイト at FORCIA #2 ゴリラの挑戦状', 'yfkpo2', '2019-09-14', 'prd_xxx, matsu7874');
ちゃんと追加できました。あとはこれを使ってアプリケーションを作ります。
※このテーブルは初期構想のものであり、今動いてるものとは異なります
コードを書く
今回はNode.jsのexpressを使います(理由:最近勉強したので)。たぶん言語はなんでもいいです。
参考:ExpressからHeroku Postgresを使う - Qiita
githubにコードをpushします。
herokuにデプロイ
参考: 【備忘録】GitHub経由でHerokuにデプロイするまでの流れ - Qiita
package.jsonに"start": "node main.js",書いてない(Node.jsアプリをHerokuにデプロイする | | KeruuWeb)とかherokuの環境変数の設定(Why is my Node.js app crashing with an R10 error? - Heroku Help)とかでだいぶ苦戦した。
その他
DB扱うときはインジェクションに注意しような👊
オイラーツアーとセグ木を使ってLCA、パスのクエリに答える
本記事では以下の問題を解きます。
N 頂点の重み付きの無向木が与えられる。
Q 回、ある辺の重みを変更するクエリと、ある2つの頂点の間の距離を求めるクエリが与えられる。
これを、1≤N≤100000, 1≤Q≤100000 で解け。
オイラーツアーは木をDFSしたときの順番で頂点を記録する手法です。オイラーツアーで記録した頂点を配列に順に入れておき、それをセグ木に対応付けます。
オイラーツアー、セグ木の概要はここではこれ以上触れません。
今回使うオイラーツアーは以下のものです。dfs以外の詳細は省きます。
vector<vector<int>> g(n); //グラフの隣接リスト vector<int> v; //オイラーツアーの頂点配列 vector<int> ind(n); //各頂点がオイラーツアー配列の何番目に最初に訪れるか void dfs(int now, int par){//今の頂点、親の頂点 ind[now] = v.size(); v.push_back(now); for(int i = 0; i < g[now].size(); i++){ if(g[now][i] != par){ dfs(g[now][i],now); v.push_back(now); } } }
根からある頂点への距離
今回は以下の木を例に説明します。

この場合オイラーツアーの配列は{1,2,3,4,3,2,5,6,5,7,5,2,1}となります。
オイラーツアー配列では、隣り合う2要素は辺で繋がれているので、辺の距離(コスト)を対応づけることができます。

では距離を計算していきましょう。
例えば根1から頂点3までの距離を考えてみると、3+1=4になってほしいです。

これは先ほどの配列で考えると、配列の先頭から、オイラーツアー配列で頂点3に対応するところまでの辺のコストの総和と考えることができます。

根1から頂点5までの距離はどうでしょうか。同じように木で考えると、根1から頂点5までの距離というのは、 (1から5の距離:ピンク) = (1から4の距離:青) - (2から4の距離:緑) + (2から5の距離:青) と考えることができます。

これを先ほどと同じように配列でうまく考えるには、帰りがけの辺のコストを負にして打ち消してあげられるようにします。

こうすると、先ほど根1から頂点3までの距離を求めたのと同様、根1から頂点5までの距離は、配列の先頭から、オイラーツアー配列で頂点5に対応するところまでの辺のコストの総和と考えることができます。

これで、根からある頂点への距離を先頭からのsumで計算できるようになりました。累積和などを使えば高速に計算できます。
任意の2つの頂点間の距離
先ほどの図において、頂点3と頂点6のパスを考えます。
根から頂点3と根から頂点6の距離は計算できるので、ここから無駄な部分を引けば、頂点3と頂点6の距離はわかります。
無駄な部分というのは、根から、頂点3と頂点6のLCAの頂点の距離です。
よって、LCAを求めることができれば、任意の2つの頂点間の距離を求めることができますね。
LCAの性質を考えると、頂点3と頂点6のLCAは、頂点3から頂点6に向かうパス上にあり、かつ、その中で根からの深さが最も小さいものです。

そのため、オイラーツアーの配列を求める際に、根の深さを記録してセグ木を作ってあげれば、区間minを計算することでLCAを求められます。
問題を解く
よって、この問題を解くには、オイラーツアー配列を作り、それに対応するコストの配列(帰りがけは逆符号とする)を作ってsumを計算できるようにして、根からの深さ配列を記録して区間minとその対応する頂点を計算できるようにすれば、計算クエリは処理できます。
変更クエリは、クエリで与えられた辺に対応するコストの配列の要素を変更すれば良いです。そのためには、各辺がコスト配列のどこに対応するのかを持っておく必要があります。これはそれぞれの辺がコストの配列のどのインデックスに対応するかを配列で持っておくなどの方法で実現できます。
最後に
この問題はHL分解を使って解くこともできます。
(HL分解を勉強しようとしたら遭遇したので:絶対に初心者でもわかるHL分解/Heavy-Light-Decomposition - Qiita)
オイラーツアーは、ある頂点の子孫に一様に操作することしかしたことがなかったので、新鮮でした。
まあHL分解のほうが木のいろんなクエリに答えることができるので、わざわざこの方法を勉強しなくてもよいという説はあります。
図作るのめんど
ブロッコリーのチヂミ
美味しかったけど、前回のチーズリゾットには負けるなあ
2種類の野菜チヂミをカフェっぽくしてみた✌️#そすうさ自炊飯#おうちで優勝 pic.twitter.com/O79Xvllfk4
— そすうさᕱᕱ(新社会人のすがた) (@wk1080id) 2020年5月10日
右のやつです。
材料(直径6cmのチヂミ8枚)
溶き卵 1個
チーズ 50g
ブロッコリーの茎(5~7mm角) 2房分(約250g)
小麦粉 大さじ3
サラダ油 適量
塩胡椒 適量
水 大さじ1
作り方
- 耐熱容器にブロッコリーの茎と水大さじ1を入れてレンジで4分加熱する
- ボウルに1と小麦粉とチーズを入れて混ぜる
- 2に溶き卵と塩胡椒を入れてよく混ぜる
- 3を4枚ずつ2回に分けて焼く。
- フライパンにサラダ油を引き、3を1/8ずつ4枚分入れ、直径6cmの薄い円形に整える
- 焼き色がついたら裏返し、両面に焼き色がつくまで焼く
- 油少量をフライパンの端から入れて強火にし、両面をカリッとさせる
ブロッコリーとコーンのミルクチーズリゾット
数学が苦手な人のための期待値DP AtCoder 第一回PAST O - 持久戦
期待値が苦手すぎるので解説を自分が理解できる粒度まで噛み砕いて書きました。
解法
dp[i] := 直前にiを出したときの残りの回数の期待値とすると
dp[max_number]は1であり、dp[0](サイコロを1度も振っていないとき)が求める値となる。
dp[i] を求める際には なる
dp[j] がわかっていればよいため、 の降順に計算する。
( のとき、出目
のあとに出目
を出すと操作が終了となり期待値は0なので)
サイコロの出目はまでであるが、出目の個数は高々
なので、座圧すると配列としてもつことができる。
出目がのサイコロを振るとき、出目は
の6通りあり、それぞれ等確率なので、
期待値は([次にa1を出したときの残りの期待値] + dp[次にa2を出したときの残りの期待値] + dp[次にa3を出したときの残りの期待値] + dp[次にa4を出したときの残りの期待値] + dp[次にa5を出したときの残りの期待値] + dp[次にa6を出したときの残りの期待値])/6に今から振る1回を足した値になる。
サイコロが1つしかない場合、目をとすると
dp[a6] = 1。
dp[5] は、 から
が出ると操作が終了(期待値0)で、
が出ると操作は終了しないので、
期待値はdp[a5] = (0 + 0 + 0 + 0 + 0 + dp[a6])/6 + 1。
dp[a4]は、 から
が出ると操作が終了で、
が出ると操作は終了しないので、
期待値はdp[a4] = (0 + 0 + 0 + 0 + dp[a5] + dp[a6])/6 + 1。
同様に、
dp[a3] = (0 + 0 + 0 + dp[a4] + dp[a5] + dp[a6])/6 + 1。
dp[a2] = (0 + 0 + dp[a3] + dp[a4] + dp[a5] + dp[a6])/6 + 1。
dp[a1] = (0 + dp[a2] + dp[a3] + dp[a4] + dp[a5] + dp[a6])/6 + 1。
dp[0] = (dp[a1] + dp[a2] + dp[a3] + dp[a4] + dp[a5] + dp[a6])/6 + 1。
サイコロが2つ以上あるとき、直前に を出した後、次に振ることができるサイコロは2つある。
どちらのサイコロを振るかは選択できるので、期待値がより大きくなる方を選べば良い。
つまり、
1つ目のサイコロを( )、2つ目のサイコロを(
)とすると
(dp[a1] + dp[a2] + dp[a3] + dp[a4] + dp[a5] + dp[a6])/6 + 1 と
(dp[b1] + dp[b2] + dp[b3] + dp[b4] + dp[b5] + dp[b6])/6 + 1 の大きい方をdp[i]の値とすればよい。
サイコロが3つ以上のときも同様で、dp[i]はその時点でのすべてのサイコロの期待値のmaxを代入すればよい。
よって、すべてのdp[i]について、個のサイコロの期待値のmaxを計算していけばよいので、
愚直にやると となる。
ここで、 番目のサイコロを振ったときの残り回数の期待値を
exp[j]とする。
exp[j]は、直前に出した目の値によって変わり、直前に を出したときは
を
をみたすサイコロ
の出目として
exp[j] = sum(dp[k])/6と表記できる。
すべてのサイコロについてexp[j]を適切に計算してあげると、
dp[i]の計算はmax(exp[j])+1で良い。
exp[j]の更新は、dp[i]の計算が終わった後、サイコロ に出目
が含まれている場合、
exp[j] += dp[i]/6をする。
max_exp = max(exp[j])という変数を作り、exp[j]が更新されるたびにmax_expを計算し直すことにすると、dp[i] = max_exp + 1と書くことができる。
まとめると、サイコロの出目を座圧し、dp[i]を の降順に計算していきながら、出目
があるサイコロ
の
exp[j]とmax_expを更新していけばよい。
exp[j]の更新は高々 回で、事前に出目
があるサイコロを
で調べられるように配列に入れて管理しておけば、dpテーブルの計算量は
である。
コード
mainのみ
signed main(void) { int n; cin >> n; vector<vector<int> > a(n,vector<int>(6)); vector<int> num;//座圧用配列 rep(i,n)rep(j,6){ cin >> a[i][j]; num.push_back(a[i][j]); } //座圧 sort(all(num)); num.erase(unique(all(num)),num.end()); int max_number = num.size(); vector<vector<int> > dice(max_number+1);//dice[i]:=出目がiのサイコロのindex rep(i,n)rep(j,6){ int ind = lower_bound(all(num),a[i][j]) - num.begin();//座圧後のindex dice[ind+1].push_back(i);//1-indexedにする } vector<double> dp(max_number+1,0),exp(n,0); double max_exp = 0; for(int i = max_number; i >= 0; i--){ dp[i] = max_exp + 1; rep(j,dice[i].size()){ //サイコロdice[i][j]に出目iが書かれている exp[dice[i][j]] += dp[i]/6.0; max_exp = max(max_exp, exp[dice[i][j]]); } } cout << shosu(10) << dp[0] << endl; }
https://atcoder.jp/contests/past201912-open/submissions/12285583
